
You can pick your private keys randomly using just a coin, pencil, and paper: toss a coin times and you have the binary digits of a random private key you can use in a bitcoin wallet. The public key can then be generated from the private key. The first and most important step in generating keys is to find a secure source of entropy, or randomness. Usually, the OS random number generator is initialized by a human source of randomness, which is why you may be asked to wiggle your mouse around for a few seconds. To create such a key, we randomly pick a bit number and check that it is less than n.
More From Medium
In programming terms, this is usually achieved by feeding a larger string of random bits, collected from a cryptographically secure source of randomness, into the SHA hash algorithm, which will conveniently produce a bit number. If the result is less than n , we have a suitable private key. Otherwise, we simply try again with another random number. Study the documentation of the random number generator library you choose to make sure it is cryptographically secure.
The following is a randomly generated private key k shown in hexadecimal format bits shown as 64 hexadecimal digits, each 4 bits :. It is approximately 10 77 in decimal. For comparison, the visible universe is estimated to contain 10 80 atoms. To generate a new key with the Bitcoin Core client see Chapter 3 , use the getnewaddress command. For security reasons it displays the public key only, not the private key.
To ask bitcoind to expose the private key, use the dumpprivkey command. The dumpprivkey command opens the wallet and extracts the private key that was generated by the getnewaddress command. It is not possible for bitcoind to know the private key from the public key unless they are both stored in the wallet.
The dumpprivkey command does not generate a private key from a public key, as this is impossible. The command simply reveals the private key that is already known to the wallet and which was generated by the getnewaddress command. You can also use the Bitcoin Explorer command-line tool see Appendix F to generate and display private keys with the commands seed , ec-new , and ec-to-wif :.
The owner of the private key can easily create the public key and then share it with the world knowing that no one can reverse the function and calculate the private key from the public key. This mathematical trick becomes the basis for unforgeable and secure digital signatures that prove ownership of bitcoin funds.
Elliptic curve cryptography is a type of asymmetric or public key cryptography based on the discrete logarithm problem as expressed by addition and multiplication on the points of an elliptic curve. Figure is an example of an elliptic curve, similar to that used by bitcoin. Bitcoin uses a specific elliptic curve and set of mathematical constants, as defined in a standard called secpk1 , established by the National Institute of Standards and Technology NIST.
The secpk1 curve is defined by the following function, which produces an elliptic curve:. Because this curve is defined over a finite field of prime order instead of over the real numbers, it looks like a pattern of dots scattered in two dimensions, which makes it difficult to visualize. However, the math is identical to that of an elliptic curve over real numbers. As an example, Figure shows the same elliptic curve over a much smaller finite field of prime order 17, showing a pattern of dots on a grid.
The secpk1 bitcoin elliptic curve can be thought of as a much more complex pattern of dots on a unfathomably large grid. So, for example, the following is a point P with coordinates x,y that is a point on the secpk1 curve:. Example shows how you can check this yourself using Python:.
Geometrically, this third point P 3 is calculated by drawing a line between P 1 and P 2. This line will intersect the elliptic curve in exactly one additional place. This tangent will intersect the curve in exactly one new point.
Generating a BTC Address with Your Own Name
You can use techniques from calculus to determine the slope of the tangent line. These techniques curiously work, even though we are restricting our interest to points on the curve with two integer coordinates! In some cases i.
- bitcoin code lookup.
- why bitcoin is going up today.
- Parameters.
- bitcoin cash price prediction 2021.
- bitcoin date de sortie.
- Your Answer;
This shows how the point at infinity plays the role of zero. Now that we have defined addition, we can define multiplication in the standard way that extends addition.
Starting with a private key in the form of a randomly generated number k , we multiply it by a predetermined point on the curve called the generator point G to produce another point somewhere else on the curve, which is the corresponding public key K. The generator point is specified as part of the secpk1 standard and is always the same for all keys in bitcoin:.
Because the generator point is always the same for all bitcoin users, a private key k multiplied with G will always result in the same public key K. The relationship between k and K is fixed, but can only be calculated in one direction, from k to K. A private key can be converted into a public key, but a public key cannot be converted back into a private key because the math only works one way. Implementing the elliptic curve multiplication, we take the private key k generated previously and multiply it with the generator point G to find the public key K :.
To visualize multiplication of a point with an integer, we will use the simpler elliptic curve over real numbers—remember, the math is the same. Our goal is to find the multiple kG of the generator point G , which is the same as adding G to itself, k times in a row. In elliptic curves, adding a point to itself is the equivalent of drawing a tangent line on the point and finding where it intersects the curve again, then reflecting that point on the x-axis. Figure shows the process for deriving G , 2G , 4G , as a geometric operation on the curve. Most bitcoin implementations use the OpenSSL cryptographic library to do the elliptic curve math.
A bitcoin address is a string of digits and characters that can be shared with anyone who wants to send you money.

Because paper checks do not need to specify an account, but rather use an abstract name as the recipient of funds, they are very flexible payment instruments. Bitcoin transactions use a similar abstraction, the bitcoin address, to make them very flexible. The bitcoin address is derived from the public key through the use of one-way cryptographic hashing. Cryptographic hash functions are used extensively in bitcoin: in bitcoin addresses, in script addresses, and in the mining Proof-of-Work algorithm.
Bitcoin Addresses and How to Use them
A bitcoin address is not the same as a public key. Bitcoin addresses are derived from a public key using a one-way function. Base58Check is also used in many other ways in bitcoin, whenever there is a need for a user to read and correctly transcribe a number, such as a bitcoin address, a private key, an encrypted key, or a script hash.
In the next section we will examine the mechanics of Base58Check encoding and decoding and the resulting representations. Figure illustrates the conversion of a public key into a bitcoin address. In order to represent long numbers in a compact way, using fewer symbols, many computer systems use mixed-alphanumeric representations with a base or radix higher than For example, whereas the traditional decimal system uses the 10 numerals 0 through 9, the hexadecimal system uses 16, with the letters A through F as the six additional symbols.
A number represented in hexadecimal format is shorter than the equivalent decimal representation. Base64 is most commonly used to add binary attachments to email. Base58 is a text-based binary-encoding format developed for use in bitcoin and used in many other cryptocurrencies. It offers a balance between compact representation, readability, and error detection and prevention. Base58 is a subset of Base64, using upper- and lowercase letters and numbers, but omitting some characters that are frequently mistaken for one another and can appear identical when displayed in certain fonts.
Or, more simply, it is a set of lowercase and capital letters and numbers without the four 0, O, l, I just mentioned. Example shows the full Base58 alphabet. To add extra security against typos or transcription errors, Base58Check is a Base58 encoding format, frequently used in bitcoin, which has a built-in error-checking code. The checksum is an additional four bytes added to the end of the data that is being encoded. The checksum is derived from the hash of the encoded data and can therefore be used to detect and prevent transcription and typing errors.
When presented with Base58Check code, the decoding software will calculate the checksum of the data and compare it to the checksum included in the code. If the two do not match, an error has been introduced and the Base58Check data is invalid. This prevents a mistyped bitcoin address from being accepted by the wallet software as a valid destination, an error that would otherwise result in loss of funds. For example, in the case of a bitcoin address the prefix is zero 0x00 in hex , whereas the prefix used when encoding a private key is 0x80 in hex.
A list of common version prefixes is shown in Table From the resulting byte hash hash-of-a-hash , we take only the first four bytes.
4. Keys, Addresses, Wallets - Mastering Bitcoin [Book]
These four bytes serve as the error-checking code, or checksum. The checksum is concatenated appended to the end. The result is composed of three items: a prefix, the data, and a checksum. This result is encoded using the Base58 alphabet described previously. Figure illustrates the Base58Check encoding process.
In bitcoin, most of the data presented to the user is Base58Check-encoded to make it compact, easy to read, and easy to detect errors. The version prefix in Base58Check encoding is used to create easily distinguishable formats, which when encoded in Base58 contain specific characters at the beginning of the Base58Check-encoded payload.
These characters make it easy for humans to identify the type of data that is encoded and how to use it. This is what differentiates, for example, a Base58Check-encoded bitcoin address that starts with a 1 from a Base58Check-encoded private key WIF that starts with a 5.
- chargeback paypal localbitcoins.
- Installation.
- momax btc ljubljana delovni cas.
- Project description!
- welcher bitcoin wallet.
- Latest commit;
Some example version prefixes and the resulting Base58 characters are shown in Table Both private and public keys can be represented in a number of different formats. These representations all encode the same number, even though they look different. These formats are primarily used to make it easy for people to read and transcribe keys without introducing errors. The private key can be represented in a number of different formats, all of which correspond to the same bit number.
Table shows three common formats used to represent private keys. Different formats are used in different circumstances. Hexadecimal and raw binary formats are used internally in software and rarely shown to users. Table shows the private key generated in these three formats. All of these representations are different ways of showing the same number, the same private key. They look different, but any one format can easily be converted to any other format.
You can use Bitcoin Explorer to decode the Base58Check format on the command line. To encode into Base58Check the opposite of the previous command , we use the base58check-encode command from Bitcoin Explorer see Appendix F and provide the hex private key, followed by the WIF version prefix Public keys are also presented in different ways, usually as either compressed or uncompressed public keys. As we saw previously, the public key is a point on the elliptic curve consisting of a pair of coordinates x,y.
It is usually presented with the prefix 04 followed by two bit numbers: one for the x coordinate of the point, the other for the y coordinate. The prefix 04 is used to distinguish uncompressed public keys from compressed public keys that begin with a 02 or a Compressed public keys were introduced to bitcoin to reduce the size of transactions and conserve disk space on nodes that store the bitcoin blockchain database.
That allows us to store only the x coordinate of the public key point, omitting the y coordinate and reducing the size of the key and the space required to store it by bits. Whereas uncompressed public keys have a prefix of 04 , compressed public keys start with either a 02 or a 03 prefix.
 How to generate custom bitcoin address
How to generate custom bitcoin address
 How to generate custom bitcoin address
How to generate custom bitcoin address
 How to generate custom bitcoin address
How to generate custom bitcoin address
 How to generate custom bitcoin address
How to generate custom bitcoin address
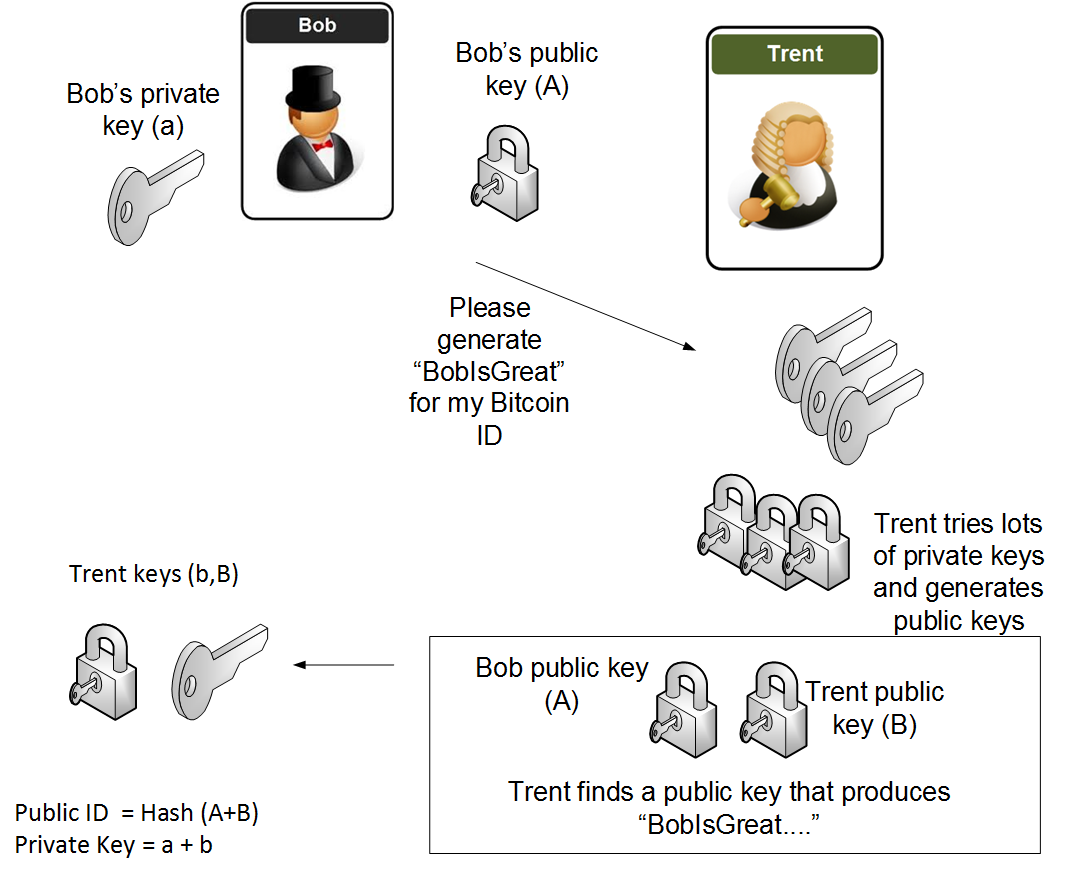 How to generate custom bitcoin address
How to generate custom bitcoin address
 How to generate custom bitcoin address
How to generate custom bitcoin address
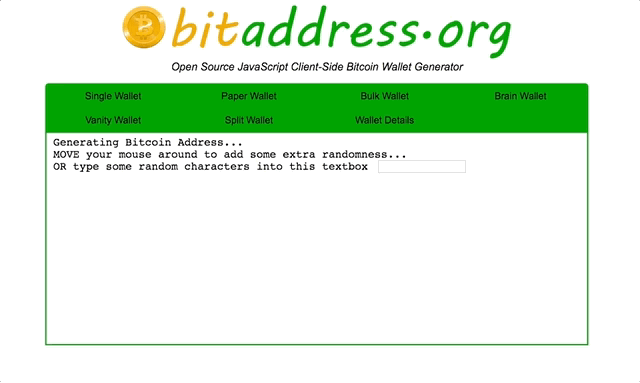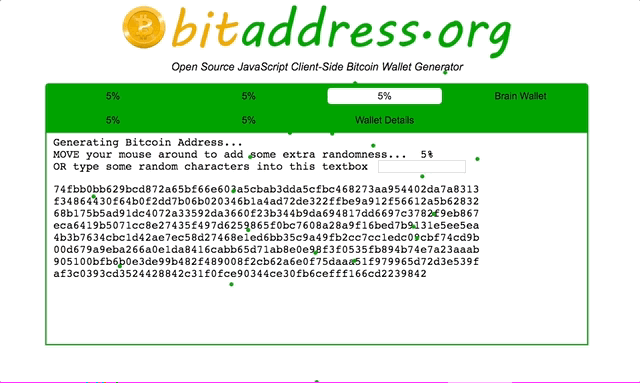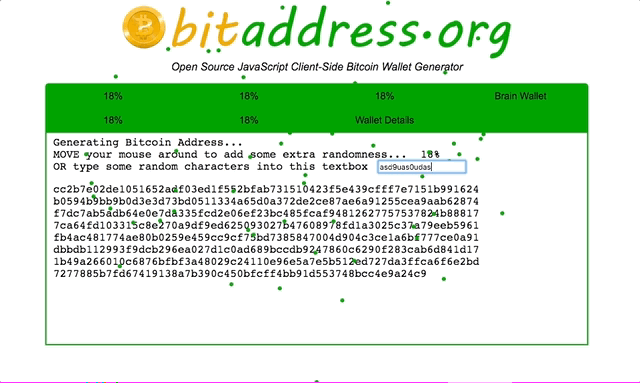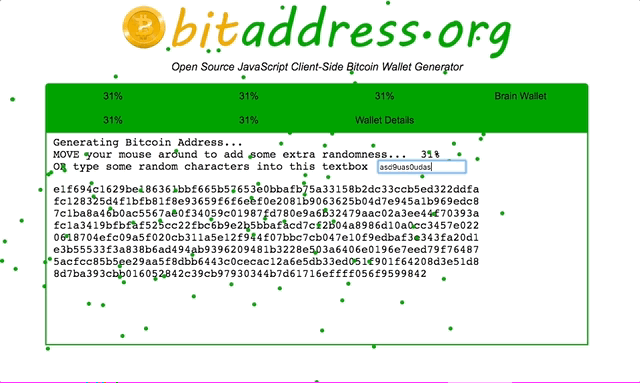 How to generate custom bitcoin address
How to generate custom bitcoin address
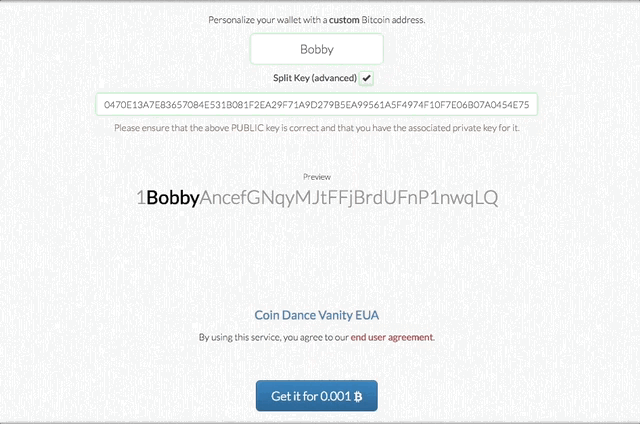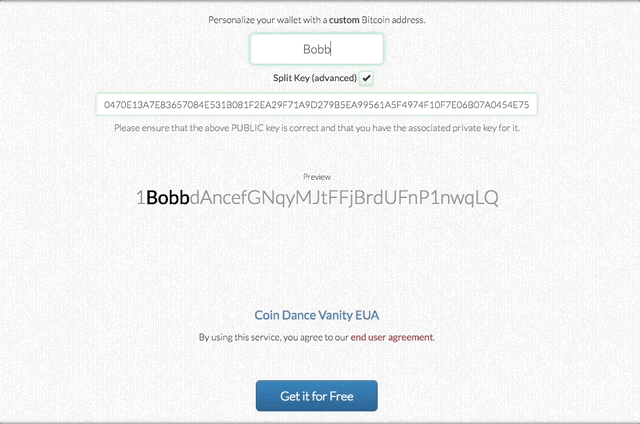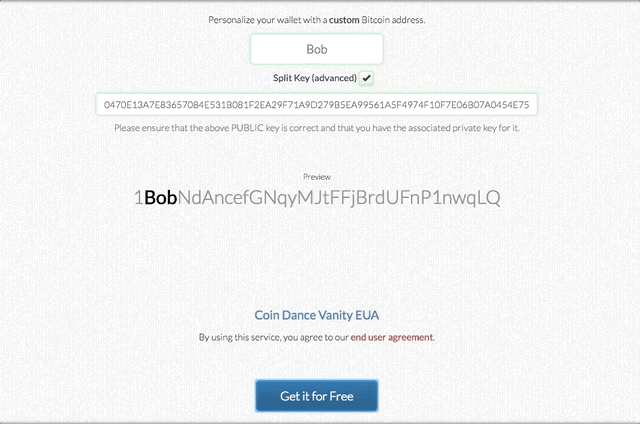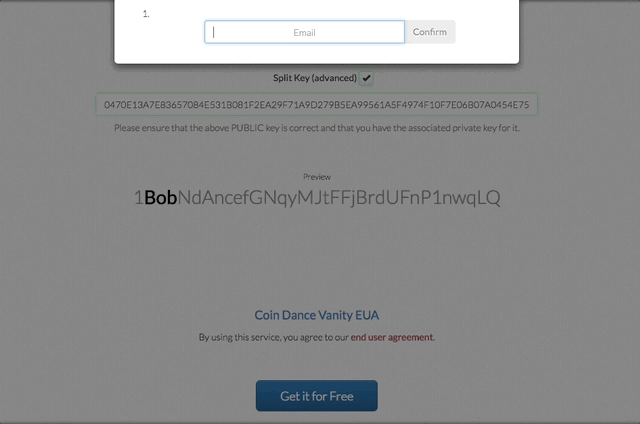 How to generate custom bitcoin address
How to generate custom bitcoin address
Related how to generate custom bitcoin address
Copyright 2020 - All Right Reserved